PostGIS - Construcción de geometrías#
Introducción#
Las funciones que se estudian en este capítulo reciben geometrías como argumentos de entrada y generan otras geometrías como salidas.
Funciones#
ST_Centroid() y ST_PointOnSurface()#
Un centroide es un punto que identifica el centro de un objeto geográfico. Puede calcularse para geometrías de líneas y de polígonos. Se utiliza para brindar una representación simplificada de una geometría más compleja. PostGIS incluye las funciones ST_Centroid() y ST_PointOnSurface() para generar centroides.
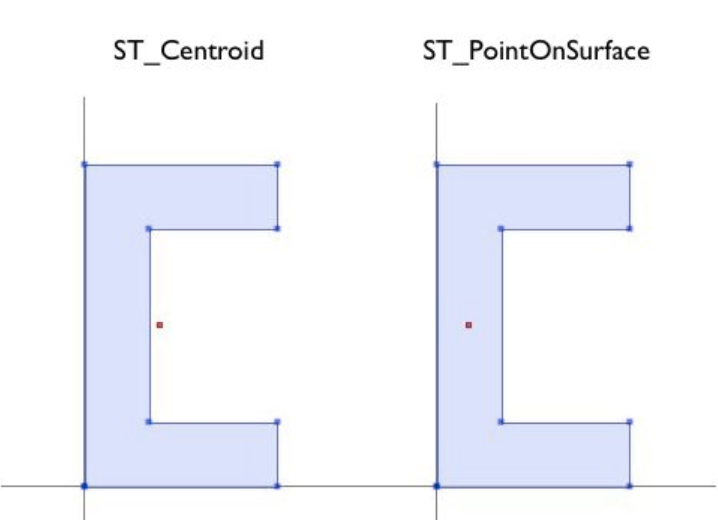
Fig. 28 ST_Centroid() y ST_PointOnSurface(). Fuente: Introduction to PostGIS.#
La función ST_Centroid(geometry) retorna un punto que está aproximadamente en el centro de masas de la geometría de entrada. Este cálculo es relativamente rápido, pero a veces es resultado no es apropiado, ya que el punto generado no necesariamente está en la geometría de entrada. Si la geometría de entrada tiene una convexidad, como en el caso de la Fig. 28, el centroide podría no estar en su interior.
La función ST_PointOnSurface(geometry) retorna un punto que se garantiza que está dentro de la geometría de entrada.
La diferencia entre ambas funciones se muestra mediante la siguiente sentencia SQL:
-- Comparación de ST_Centroid() y ST_PointOnSurface() para una geometría convexa
SELECT
ST_Intersects(geom, ST_Centroid(geom)) AS dentro_centroid,
ST_Intersects(geom, ST_PointOnSurface(geom)) AS dentro_pointonsurface
FROM
(
VALUES('POLYGON ((30 0,30 10,10 10,10 40,30 40,30 50,0 50,0 0,0 0,30 0))'::geometry)
) AS t(geom);
dentro_centroid | dentro_pointonsurface
-----------------+-----------------------
f | t
En la sentencia SQL anterior, t(geom) es una tabla derivada, la cual es una expresión que se define en la cláusula FROM y se trata como una tabla temporal en la consulta, pero no se almacena en la base de datos.
ST_Buffer()#
Un buffer es un polígono creado alrededor de una geometría, ya sea otro polígono, una línea o un punto.
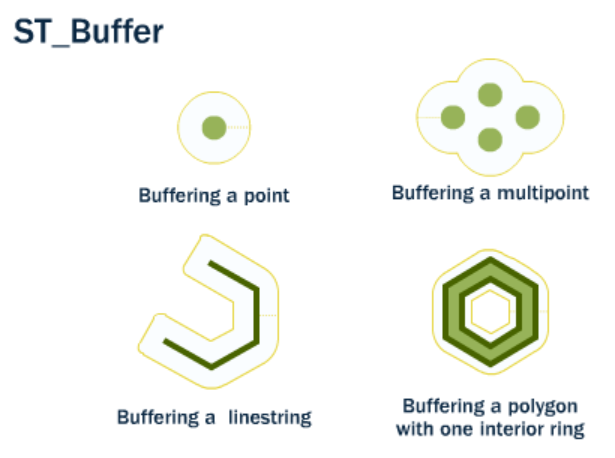
Fig. 29 ST_Buffer(). Fuente: Introduction to PostGIS.#
La función ST_Buffer(geometry, distance) toma como entradas una geometría y una distancia y retorna otra geometría con un límite a la distancia especificada de la geometría de entrada.
La siguiente sentencia SQL crea un buffer de 100 m alrededor de la ruta 27 y lo guarda en una tabla.
-- Buffer alrededor de la ruta 27
CREATE TABLE buffer_27_100 AS
SELECT ST_Buffer(geom, 100) AS geom
FROM red_vial_200k
WHERE num_ruta = '27';
Y la siguiente consulta despliega las edificaciones prominentes situadas completamente dentro del buffer generado con la sentencia anterior.
-- Edificaciones prominentes situadas completamente dentro del buffer
nom_objeto | nombre
------------------------+------------------------------------
CENTRO EDUCATIVO | Escuela La Balsa
EDIFICIO RELIGIOSO | Iglesia
EDIFICIO GUBERNAMENTAL | Federaci≤n Costarricense de F·tbol
EDIFICIO RELIGIOSO | Iglesia
ST_Buffer() también acepta distancias negativas para geometrías de polígonos. En ese caso, construye un polígono inscrito. En el caso de líneas y puntos, retorna una geometría vacía.
ST_Intersection()#
La intersección de geometrías, llamada también overlay (superposición), es otra operación muy común en procesamiento de datos espaciales.
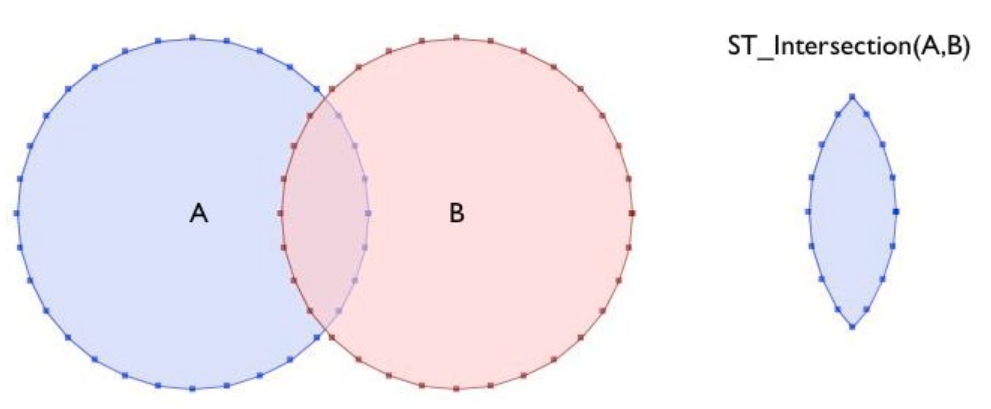
Fig. 30 ST_Intersection(). Fuente: Introduction to PostGIS.#
La función ST_Intersection(geometry A, geometry B) retorna el polígono, línea o punto que las geometrías de entrada tienen en común. Si las geometría son disjuntas, retorna una geometría vacía.
La siguiente consulta obtiene la intersección de los dos círculos que se muestran en la Fig. 30.
-- Intersección de dos círculos generados con ST_Buffer()
SELECT ST_AsText(ST_Intersection(
ST_Buffer('POINT(0 0)', 2),
ST_Buffer('POINT(3 0)', 2)
));
POLYGON((1.961570560806461 -0.390180644032256,1.847759065022574 -0.76536686473018,1.66293922460509 -1.111140466039204,1.5 -1.309682485677078,1.337060775394909 -1.111140466039204,1.152240934977426 -0.76536686473018,1.038429439193539 -0.390180644032257,1 -2.449212707644754e-16,1.038429439193539 0.390180644032257,1.152240934977426 0.765366864730179,1.337060775394909 1.111140466039204,1.5 1.309682485677078,1.66293922460509 1.111140466039204,1.847759065022573 0.765366864730181,1.961570560806461 0.390180644032257,2 0,1.961570560806461 -0.390180644032256))
Ejercicio:
En un SIG, grafique los círculos de la sentencia anterior y su intersección.
ST_Union()#
ST_Intersection() crea una nueva geometría con líneas de ambas entradas. La función ST_Union() realiza lo contrario: toma las geometrías de entrada y elimina las líneas comunes.
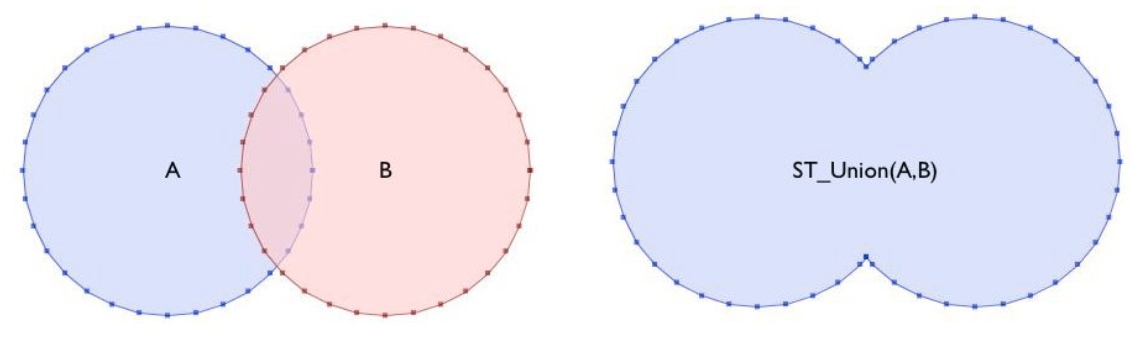
Fig. 31 ST_Union(). Fuente: Introduction to PostGIS.#
Hay dos formas para la función ST_Union():
ST_Union(geometry A, geometry B): recibe dos geometrías y retorna su unión. Por ejemplo, los círculos que se intersectaron en la sección anterior pueden unirse con:
-- Unión de dos círculos generados con ST_Buffer()
SELECT ST_AsText(ST_Union(
ST_Buffer('POINT(0 0)', 2),
ST_Buffer('POINT(3 0)', 2)
));
El resultado se muestra en la Fig. 31.
ST_Union(geometry): toma todas las geometrías de un conjunto (ej. de una tabla, de una consulta) y retorna su unión. Esta versión “agregada” puede usarse conjuntamente con la cláusula
GROUP BYpara generar subconjuntos agrupados de geometrías individuales. Por ejemplo, la siguiente sentencia SQL une las geometrías de los cantones en provincias.
-- Unión de cantones en provincias
SELECT provincia, ST_Union(geom) AS geom
FROM cantones
GROUP BY provincia;
Ejercicio:
Ejecute la sentencia anterior en un SIG y observe el resultado.
Ejercicios#
Genere capas de centroides para las provincias de Costa Rica:
Con
ST_Centroid().Con
ST_PointOnSurface(). Despliegue ambas capas en un mapa, junto con la capa de provincias, para así apreciar las diferencias.
Con
ST_Centroid()yST_PointOnSurface()genere los centroides de la ruta 32. Despliegue ambos en un mapa, junto con la geometría de la ruta 32.Obtenga la lista de especies de mamíferos con mayor riesgo de atropello en la ruta 32:
Con
ST_Buffer(), genere un buffer de 5 km alrededor de la ruta 32.Con base en los registros de presencia de mamíferos agrupados en el portal de GBIF (https://doi.org/10.15468/dl.vmdyxe), genere la lista de registros de presencia de mamíferos que se encuentran dentro del buffer. Excluya los mamíferos voladores (murciélagos, orden Chiroptera).
A partir del resultado del punto anterior, genere la lista de las 10 especies con más registros.
Con
ST_Intersection(), genere los polígonos de ASP que se intersectan con el cantón de Sarapiquí.Con
ST_Union()una los cantones en provincias y calcule el área para cada una. Compare el resultado con las áreas de la capa de provincias que publica el IGN.Con
ST_Union()una las provincias de Costa Rica en un solo polígono. Luego, obtenga los centroides de ese polígono con las funcionesST_Centroid()yST_PointOnSurface().
